Squaring the Circle Using a Special Kind of Polygon Based on the "Holy Triangle" 3-4-5 and a Sequence of Further So-called Pythagorean Triples - A Method Probably Discovered by Imhotep and Refined by the Unknown Builder of the Great Pyramid at Giza
by Franz Gnaedinger, Zürich, 1996
Please imagine a square inscribed in a circle. Let the square pass over into an octagon, a regular 16-gon, 32-gon, 64-gon ... As the number of corners increases the polygon slowly converges with the circle. The side lengths, perimeters and areas of the subsequent figures can be calculated by repeatedly applying the formula of Pythagoras and computing a chain of square roots which gets longer and longer. This method of "squaring the circle" was discovered by Antiphon of Athens (c.430 BC) and further developed by Archimedes of Syracuse (283-212 BC) who found that the ratio of the circumference of the circle to its diameter is less than 3 1/7 and greater than 3 10/71. Archimedes even wrote a book on the circle, which was lost while his method survived. In his lost work he must have mentioned Antiphon and his many other precursors, among them Deinostratus, Hippias of Elis, Hippocrates of Chios, Bryson of Herakleia, Anaxagoras of Clezomenae and perhaps some others by now forgotten. I wonder if he also knew of a simpler and probably much older way of solving the problem, a method based on the Holy Triangle 3-4-5 and a sequence of further triples which satisfy the formula axa + bxb = cxc. This formula is known under the name of Pythagoras while the triples of whole numbers which are derived from it are called Pythagorean triples. However, such triples had already been used in ancient Mesopotamia as early as 2000 BC, and even earlier by the pyramid builders of ancient Egypt, first of all by Imhotep, the most ingenious vizier and architect of Pharaoh Djoser who reigned around 2600 BC and had built for his glory and eternal life the monumental yet also beautiful and even graceful Step Pyramid Complex at Saqqara near the former city of Memphis.
A new way to square the circle that may have been a very old one
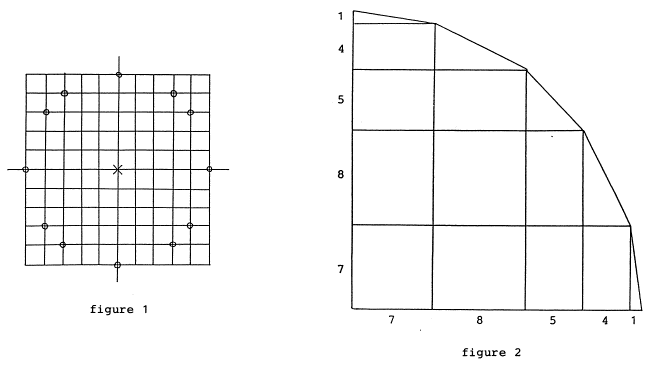
Please imagine a circle of radius 5 x 5 x 5 x 5 ... = 5, 25, 125, 625 ... units or subunits. Combine the circle with the cross of the axes and a grid of 10 x 10, 50 x 50, 250 x 250, 1250 x 1250 ... squares. The axes define the center of the circle and 4 points of the periphery. 8, 12, 20, 28 ... further points are defined by the following triples beginning with the Holy Triangle:
3-4-5 = 15-20-25 = 75-100-125 = 275-500-625 ...
7-24-25 = 35-120-125 = 175-600-625 ...
44-117-125 = 220-585-625 ...
336-527-625 ...
The subsequent triples 1, 2, 3, 4, 5, 6 ... can be derived using
two rather simple formulas:
triples 1, 3, 5 ... be termed a-b-c (a smaller than b) triples 2, 4, 6 ... be termed A-B-C (A smaller than B) A-B-C follows a-b-c: A = 4b - 3a B = 3b + 4a C = 5c a-b-c follows A-B-C: a = 3B - 4A b = 4B + 3A c = 5CThe axes and subsequent triples define 12, 20, 28, 36 ... points of the periphery. If we join them up in turn with lines we obtain a sequence of polygons with 12, 20, 28, 36 ... unequal sides. As the number of sides increases, the polygon slowly converges with the circumscribed circle.
Figure 1 shows the grid 10 by 10 and the corners of the first
polygon.
Figure 2 shows a quarter of the second polygon.
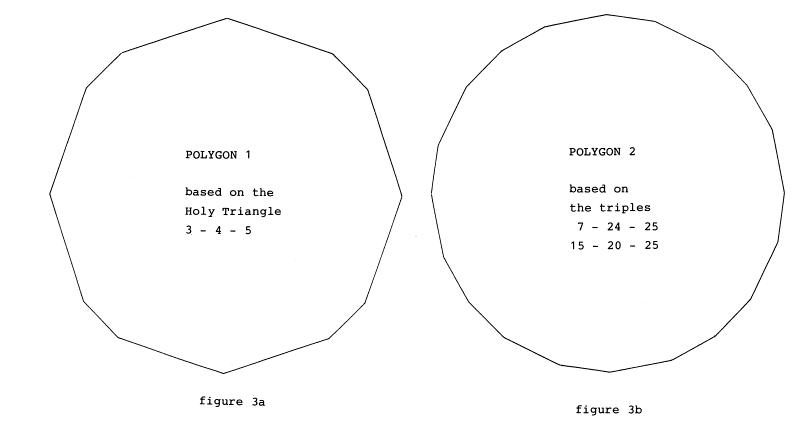
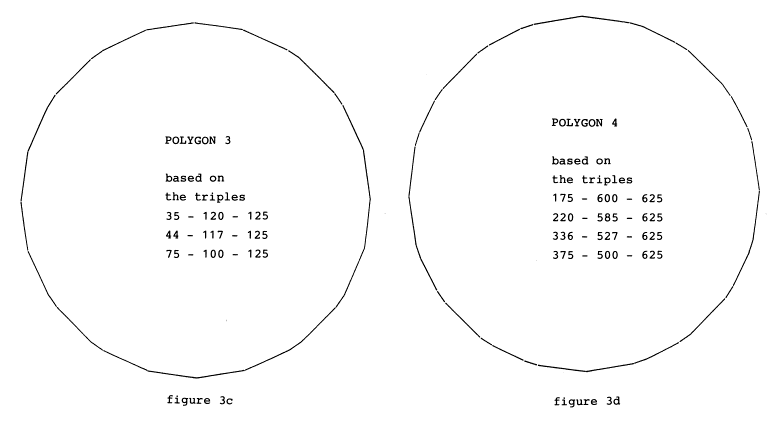
Figures 3a - 3d show the first four polygons.

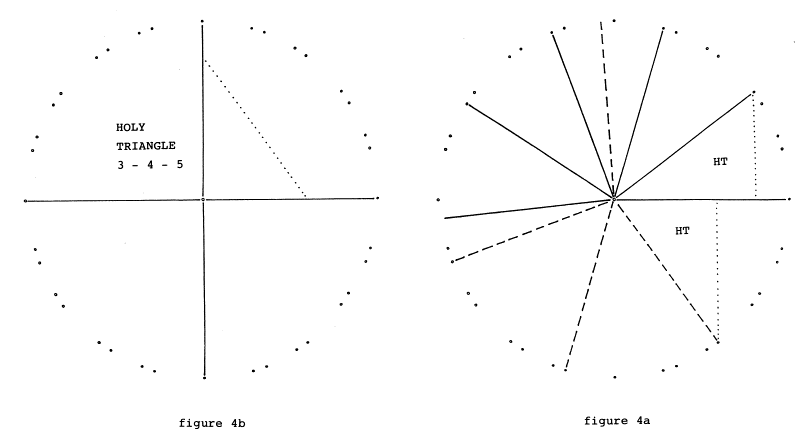
[I wish to thank the Assistence Group 1, Department of Mathematics, ETH Zurich, for proving that the ratio alpha/beta is transcendental. Hence the half lines rotating in alpha angle stages will never touch the same point twice. Furthermore we may assume that the marked corners will cover the periphery of the circle in equal density, our polygons thus truly passing over into the form of the circle. - For example, polygon 41 has 244 longer and 88 shorter sides. The radius measures 541 = 45,474,735,088,646,411,895,751,953,125 units or subunits while the ratio of the perimeter to the diameter is 3.14154...]
How long are the sides of our polygons? If we knew this we would be able to calculate their perimeters and approximate the periphery of the circle (slightly more than the perimeter of an inscribed polygon) and even its area (half the perimeter of the "final" polygon multiplied by half its diameter).
The squares of the side lengths of the first four polygons are derived as follows:
1 x 1 + 1 x 1 = 2
1 x 1 + 2 x 2 = 10 = 2 x 5
1 x 1 + 7 x 7 = 5 x 5 + 5 x 5 = 50 = 5 x 5 x 2
4 x 4 + 8 x 8 = 80 = 4 x 4 x 5
35x35 + 35x35 = 31x31 + 17x17 = 25x25 = 1,250 = 125x125x2
9x9 + 3x3 = 90 = 3x3x2x5
175x175 + 25x25 = 125x125 + 125x125 = 31,250 = 125x125x2
116x116 + 58x58 = 16,820 = 58x58x5
45x45 + 15x15 = 39x39 + 27x27 = 2,250 = 15x15x2x5
Hence the side lengths are multiples of the square root of 2 = sr2, the square root of 5 = sr5 and the square root of 2 multiplied by the square root of 5 = sr2 x sr5 or sr2 sr5:
1 sr2 1 sr2 sr5
5 sr2 4 sr5
25 sr2 3 sr2 sr5
125 sr2 58 sr5 15 sr2 sr5
The same is true for every following polygon: the sides are
whole number multiples of sr2, sr5 and sr2 sr5. Hence we are
able to square the circle by means of just two square roots.
How do we derive these roots? From triples with minor flaws.
Please look at the following examples:
5 x 5 + 5 x 5 = 7 x 7 + 1
12 x 12 + 12 x 12 = 17 x 17 - 1
29 x 29 + 29 x 29 = 41 x 41 + 1
70 x 70 + 70 x 70 = 99 x 99 - 1
A square measuring 5 x 5, 12 x 12, 29 x 29, or 70 x 70 units possesses a pair of diagonals measuring roughly 7, 17, 41 or 99 units respectively. Hence the ratios 7/5, 17/12, 41/29 and 99/70 are approximate values for the square root of 1x1 + 1x1 = 2.
4 x 4 + 8 x 8 = 9 x 9 - 1
17 x 17 + 34 x 34 = 38 x 38 + 1
72 x 72 + 72 x 72 = 161 x 161 - 1
A rectangle measuring 4 x 8, 17 x 34 or 72 x 144 units possesses a pair of diagonals measuring roughly 9, 38 or 161 units respectively. Hence the ratios 9/4, 38/17 and 161/72 are approximate values for the square root of 1x1 + 2x2 = 5.
The pseudo-triples 5'5'7, 12'12'17, 29'29'41, 70'70'99
demonstrate a regularity: 5 + 7 = 12, 12 + 17 = 29, 29 + 41
= 70. We use this to draw up a number column which requires
only simple addition and periodic multiplication by a factor
of 2:
1 1 2
2 3 4
5 7 10
12 17 24
29 41 58
70 99 140
... ... ...
The ratios 10/7 or 17/12 are workable values for the square root of 2, while the ratio 99/70 = 1.41428... is an excellent approximation of the precise value 1.41421...
(Incidentally: the duplication of the cube was a another famous problem. It may be solved using a number column beginning with the lines 1-1-1-2, 2-2-3-4, 4-5-7-8, 9-12-15-18, 3-4-5-6, 7-9-11-14 ... 400-504-635-800 ...)
We may proceed in a similar way to find the square root of 5:
1' 1'' 5
2 6 10
1' 3'' 5
4 8 20
2' 4'' 10
1 2 5
3' 7'' 15
10 22 50
5' 11'' 25
16 36 80
8' 18'' 40
4 9 20
13' 29'' 65
42 94 126
21' 47'' 105
68 152 340
34' 76'' 170
17 38 85
55' 123'' 275
178 398 890
89' 199'' 445
288 644 1440
144' 322'' 720
72 161 360
... ... ....
The ratio 18/8 = 9/4 is a workable value and the ratio 322/144
= 161/72 = 2.236111... is a fairly good approximation of the
square root of 5 = 2.236067...
The marked numbers 1' 1' 2' 3' 5' ... and 1'' 3'' 4'' 7'' 11'' ... represent golden sequences of the form a, b, a + b = c, b + c = d, c + d = e ... By arranging them in lines one above the other we may approximate the square root of 5 more quickly:
1 3 4 7 11 18 29 47 76 123 199 322 ...
1 1 2 3 5 8 13 21 34 55 89 144 ...
A still faster approximation is carried out by adding numerators and denominators of roughly the same size:
5 = 5/2 x 2/1 = 5/2 x 4/2 * (5+4) / (2+2) = 9/4
5 = 20/9 x 9/4 = 20/9 x 18/8 * (20+18)/ (9+8) = 38/17
5 = 85/38 x 38/17 = 85/38 x 76/34 * (85+76)/(38+34) = 161/72
The ratios 9/4, 38/17 and 161/72 again represent the triples
with minor flaws rendered above.
[I wish to thank Dr. Christoph Poeppe from the University of Heidelberg for confirming that my number columns do in fact approximate the respective square roots.]
Now let us see what can be done with our numbers.
The perimeters of the first four polygons are given by the sums
P1 = 4 x 1 sr2 + 8 x 1 sr2 sr5
P2 = 12 x 5 sr2 + 8 x 4 sr5
P3 = 20 x 25 sr2 + 8 x 3 sr2 sr5
P4 = 12 x 125 sr2 + 8 x 58 sr5 + 16 x 15 sr2 sr5
Calculating them by the ratios
sr2 between 140/99 and 99/70
sr5 between 360/72 and 161/72
sr2 sr5 between 800/253 and 253/80
and dividing the results by the diameters we obtain
P1/D1 = between 3.0953... and 3.0967...
P2/D2 = between 3.1280... and 3.1282...
P3/D3 = between 3.1318... and 3.1321...
P4/D4 = between 3.1340... and 3.1343...
The ratios gradually approach the number of the circle 3.14159... called "pi" by William Jones and Leonhard Euler.
What else can be done with our method? We may improve on it
by means of a simple consideration:
The circumference of the circle is always slightly larger
than the perimeter of any inscribed polygon. We may hope to
counterbalance this by choosing ratios for sr2 and sr5 which
are slightly higher than these numbers:
10/7, 17/12 ... for sr2
9/4, 65/29 ... for sr5
The perimeter of the first polygon is given by the sum
4 sr2 + 8 sr2 sr5
We take 10/7 for sr2 and 9/4 for sr5 and obtain
4 x 10/7 + 8 x 10/7 x 9/4 = 40/7 + 180/7 = 220/7
Dividing the perimeter 220/7 by the diagonal or diameter 10 we obtain
22/7 = 3 1/7 = 3.1428...
which is a famous value for pi.
The perimeter of the second polygon is given by the sum
12 x 5 x sr2 + 8 x 4 x sr5
This time we select 17/12 for sr2 and again 9/4 for sr5:
12 x 5 x 17/12 + 8 x 4 x 9/4 = 85 + 72 = 157
Dividing this number by the diameter 50 we obtain
157/50 = 3.14
22/7 equals 154/49, which is nearly the same as 157/50. Adding both numerators and denominators we find
(154 + 157) / (49 + 50) = 311/99 = 3.1414...
The perimeter of the fourth polygon is given by the sum
12 x 125 sr2 + 8 x 58 sr5 + 16 x 15 sr2 sr5
We fill in 17/12 for sr2 and 65/29 for sr5:
12x125x17/12 + 8x58x65/29 + 16x15x17/12x65/29
= 2125 + 1040 + 762 + 2/29
We let go of the small fraction 2/29 and get the perimeter
2125 + 1040 + 762 = 3927. Dividing this number by the
diameter 1250 we obtain
3927 / 1250 = 3.1416
which is a fairly close approximation of pi = 3.14159...
We found sr2 and sr5 using number columns. Can we possibly approximate the number of the circle in a similar way? Here is at least a number game which delivers some nice values:
4 (+ 3) 7 10 13 16 19 22 25
1 (+ 1) 2 3 4 5 6 7 8
3 (+ 22) 25 47 69 91 113 135 157 179
1 (+ 7) 8 15 22 29 36 43 60 57
201 223 245 267 289 311 333 355 (3927) 377
64 71 78 85 92 99 106 113 (1250) 120
Again we find the ratios 22/7, 157/50 and 311/99. The ratio
3927/1250 is slightly smaller than 377/120 and slightly greater
than 355/113 = 3.1415929... which is by far the best approximate
value of pi = 3.1415926...
Another approximation formula is 3 + 1/10 of sr2. Filling in
the numbers in the column for sr2 we obtain
3 + 1/10 of 2/1 = 16/5 = 3.2
3 + 1/10 of 1/1 = 31/10 = 3.1
3 + 1/10 of 4/3 = 47/15 = 3.1333...
3 + 1/10 of 3/2 = 63/20 = 3.15
3 + 1/10 of 10/7 = 22/7 = 3.1428...
3 + 1/10 of 7/5 = 157/50 = 3.14
3 + 1/10 of 24/17 = 267/85 = 3.14117...
3 + 1/10 of 17/12 = 377/120 = 3.141666...
3 + 1/10 of 58/41 = 644/205 = 3.14146...
3 + 1/10 of 41/29 = 911/290 = 3.14137...
3 + 1/10 of 140/99 = 311/99 = 3.1414...
3 + 1/10 of 70/99 = 1299/700 = 3.141428...
And there is of course the magic formula pi = phi x phi x 6/5. The golden number phi = 1.6180339... can be approximated using a golden sequence, for example the so-called Fibonacci Sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 ... . Filling in some ratios obtained from this sequence we come up with:
55/34 x 34/21 x 6/5 = 22/7 = 3.1428...
89/55 x 55/34 x 6/5 = 267/85 = 3.14117...
144/89 x 89/55 x 6/5 = 864/275 = 3.141818...
233/144 x 144/89 x 6/5 = 1398/445 = 3.141573...
377/233 x 233/144 x 6/5 = 377/120 = 3.141666...
610/377 x 377/233 x 6/5 = 732/233 = 3.14163...
Instead of using our common formulas and the number pi we may combine two measures
a = 7 or about 7 or varying around 7
b = 11
a/b = 7/11 or pi/2 or some other ratio
The combined measures a and b enable us to render some complicated formulas simple:
diameter of a circle = a, periphery = 2b
radius = a, area = 2ab
diameter of a sphere = a, surface = 2ab,
volume of 3 spheres = aab
volume of one sphere = volume of a pyramid
given by the base a x a and the height b
golden minor of 5a = 3b
side of a square = 10a, diagonal = 9b
side of a square = 9b, diagonal = 20a
...
A pyramid of base a x a and height b has the same volume as a sphere of diameter b. Even more interesting is the inverse pyramid of height a and base b x b:
height = a = 33.32 cm = 7/11 of a cubit
base = b = 52.36 cm = one cubit
There is a real pyramid which corresponds to our model:
the Great Pyramid at Giza, probably built around 2450 BC
for Pharaoh Khufu.Some one hundred years ago the English scholar John Taylor discovered an exciting relationship in the measurements of this pyramid.
Please imagine a large circle, the vertical diameter of which is given by the height of the original, undamaged building as shown in figure 5. What is the circumference of the circle? Twice the base of the pyramid. And what is the area of the circle? The same as that of the section area of the pyramid!
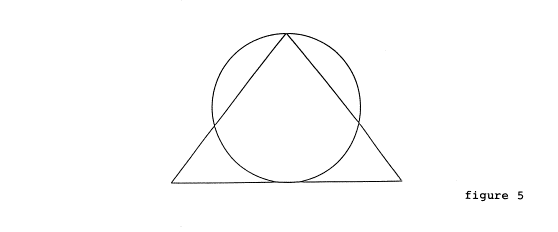
Georges Goyon provided the following measurements:
original height = 280 cubits [or 440 a]
original base = 440 cubits [or 440 b]
Hence the base measurement, doubled, would have been 880 c. Dividing this by 280 c we obtain 880 c / 280 c = 22/7.
A mere coincidence, according to most Egyptologists. For it
is well known that the pyramid builders of the Old Kingdom were
neither able to calculate the golden number phi nor the number
of the circle.
Or were they?
The golden number can easily be approximated by golden
sequences requiring only simple additions. Even the number
of the circle can be calculated in a rather simple way offering
some very good approximate values from the initial polygons.
Our method requires a) the knowledge of the Holy Triangle 3-4-5
and a sequence of further triples which are derived from two
rather simple formulas, b) the square roots of 2 and 5 which
are approximated by means of our simple number columns, and
c) a list of the squared numbers up to 625 x 625. These numbers
can be simply compiled by adding up the sequence of odd numbers:
1, 1 + 3 = 4, 1 + 3 + 5 = 9, 1 + 3 + 5 + 7 = 16 ... It is true
that you have to add up a lot of numbers before you reach 6252
= 390,625. However, what is the adding up of a few hundred
numbers in comparison with the piling up of the one or two
million blocks required for the building of a pyramid?
You may be astonished to hear that all the necessary elements and even the most important numbers of our method are present (and preserved) in the Step Pyramid Complex of Djoser at Saqqara and in the large pyramids of Khufu and Khafre at Giza.
According to Wolf Meyer Christian the following triples are
combined in the digit-measurements of a single sarcophagus
embedded in the southern area of the Djoser Complex:
(3-4-5 =) 60-80-100 = 66-88-110 = 81-108-135 = 132-176-220
= 135-180-220, (8-15-17 =) 80-150-170, (20-21-29) = 80-84-116,
(28-45-53 =) 84-135-159, 48-55-73, 55-132-143 and 84-135-159.
According to the same author the whole area is covered by
a grid of invisible squares governed by the numbers 12 and 17
as the side and diagonal. Hence the square root of 2 was
approximated by the ratio 17/12.
In the King's Hall a drawing was found on a piece of wood
which depicts an arc or possibly even a quarter of a circle
measured by vertical lines anticipating our co-ordinates.
Jean-Philippe Lauer, excavator of the Djoser Complex, found
a Holy Triangle measuring 15-20-25 cubits in the King's Chamber
of the Great Pyramid at Giza. The most impressive room measures
10 x 20 x 11.18 cubits while 8 Holy Triangles are combined from
the 15-cubit diagonals of the small walls, the 20-cubit lengths
of the chamber and the 25-cubit diagonals of the chamber.
Georges Goyon defined the Great Pyramid as follows:
height / half the base = 14/11
height / half the diagonal of the base = 9/10
Hence:
diagonal of the base / base = 140/99
half the diagonal of the base / base = 99/70.
The section area is 280 b x 220 b = 440 a x 220 b or
approximately 390 a x 390 a. These measurements define a square.
Its diagonals measure 351 b while the ratio of the diagonal
to the side is 351 b / 390 a = 9b / 10a = 9x11 / 10x7 = 99/70.
The square has the same area as the Taylor Circle. Hence the
square root of pi is approximately 39/22. The square root of
this ratio is roughly 4/3 which corresponds to the value (16/9)2
for pi used in the famous Rhind Papyrus written by one Ahmose
in 1650 BC.
The angle of the downleading gangway is given as 26¯ 34' 23"
while the (oblique) height of the gangway measures 120 cm
(according to Rainer Stadelmann). Hence the tangent is 1/2.
The vertical distance from the ceiling to the floor is 72 digits,
the horizontal distance 2 x 144 d and the respective oblique
part of the ceiling or the floor 161 d (1 digit being 1.87 cm).
Thus, the square root of 5 has been approximated by the ratio
161/72.
Finally, the pyramid of Khefre is based upon the Holy Triangle
found in the section area:
half the base = 3 x 68.5 cubits
vertical height = 4 x 68.5 cubits
oblique height = 5 x 68.5 cubits
May we assume that our method of squaring the circle was orginally discovered by Imhotep? and refined by some of his followers? above all by the unknown builder of the Great Pyramid at Giza? although it was later forgotten for reasons at which we may only guess?
Why, though, should a pyramid builder concern himself with the circle at all when the form of his building consists of triangles and a square?
The base of the Great Pyramid is or was a perfect square facing
south - Middle and Upper Egypt
north - Lower Egypt
east - Arabian Desert
west - Libyan Desert
As part of the ground, the square of the base may have been
a symbol for the earth, whereas the so-called pyramidion,
the possibly gilded top stone, pointed up to the sky. The sky
was always seen as a vault or a hemisphere, a round form defined
by arcs and circles. The sun appears as a tiny yet perfect
circle, and so does the full moon. Most of the celestial bodies
are seen to be moving in arcs while the "imperishable" stars
near the northern pole, then Alpha Draconis, orbit in circles.
The rainbow appears as an arc and at rare times, when the sun
is very high, as a double ring.
The square was presumably the symbol of the earth while
the circle, arcs and hemisphere may have been symbols of the
sky. Finding a way to square the circle may thus have been a
way to join earth and heaven.
On one point all scholars seem to agree: the Egyptian pyramids
on the western bank of the river Nile are symbols for the Primary
Hill rising above the Primary Water.
Out of the hill rose the sky goddess Hathor, appearing as
a cow carrying the golden disk of the sun in the bow of her
horns.
The solar disk was both the sun and the sun god Re, whose
hieroglyph was a circle.
May the large circle discovered by John Taylor thus have been
the symbol of Re emerging from the Primary Hill?
And could there possibly be another geometric form representing
the sky once enclosed in the same hill?
Let us take another look at the measurements of the pyramid.
The huge building demonstrates a simple form defined by a simple ratio. But in this simple form and ratio are combined two special pyramids of the highest mathematical interest:
If we lower the original pyramid by only 8.15 cm we obtain
the Golden Pyramid according to Herodot and the priests of
Memphis. This pyramid is defined as follows: the square of the
height has the same area as one side.
Approximating the Golden Pyramid
using whole numbers we obtain the Jarolimek Pyramid. Its oblique
height is 356 cubits while the ratio of this measurement and
half the base is 356/220 = 89/55. These numbers come from the
golden sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ... The
length of the ceiling of the Great Gallery measures 89 cubits
while the respective ascent is 39 cubits and the respective
horizontal measurement 80 cubits according to the triple
39-80-89.
If we raise the original pyramid by only 5.9 cm we obtain
the Taylor Pyramid based on the number of the circle and
discussed above.
Using the ratio 22/7 for pi we obtain the simple
Goyon Pyramid. Using the combined measures "a" and "b" the height
is 440 a and the base 440 b. The length of the gallery ceiling
is given as the height of the pyramid divided by the number
of the circle = 440 a / 22/7 = 140 a. The respective ascent
is 39.2 b while the respective horizontal measurement is again
80 b. These numbers are derived from a magic triangle based
on the tripel 529'1100'1225 with only a minor flaw:
44 x 44 = oblique height
49 x 44 = vertical height (39.2 a)
44 x 100 = horizontal length (80 b)
49 x 100 = oblique length (140 a)
cosine = 44 / 49 = 4 b / 7 a
One ideal ceiling ascends 39 b on 80 b, the other 39.2 b on 80 b. The middle ascent is 39.1 b on 80 b and its angle is 26¯ 2' 49" while according to Rainer Stadelmann the angle of the gallery built measures 26¯ 2' 30" - a difference of only 19 seconds.
(Incidentally, the combined measures "a" and "b" and their subunits reveal an astonishingly simple construction plan for the Great Gallery and its five dimensions, which cannot however be discussed here.)
In the Beginning there was the Primordial One bringing forth
polarity, which creates all the many forms, things and living
beings. According to Erik Hornung the concept of polarity and
the number 2 emerging from the Primordial One were important
in the thinking of the ancient Egyptians, while according to
Jan Assmann the latter's main philosophical concern regarding
creation was the appearance of the Many from the One.
A mathematical solution to this problem may have been realized
in the Great Pyramid: there is found the simple Goyon Pyramid
which may symbolize the Primary Hill as well as the Primordial
One. The Goyon Pyramid gives way to a pair of special pyramids
based on the golden number and the number of the circle. These
two pyramids offer a kind of a mathematical cosmos (if I may
say so) and even two additional yet imaginary forms: the large
circle discovered by John Taylor, shown in figure 5 above, and
the golden hemisphere shown in figure 6 below:
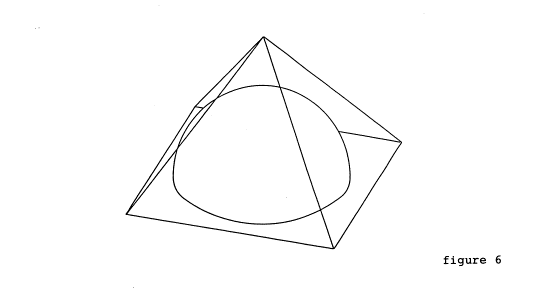
The imaginary vault stands on the base of the pyramid and touches the four sides of the building from within. The radius of the hemisphere is the golden major of the height of the pyramid while the surface touches the four sides in the golden minor of the same measurement. The golden minor and major of 280 cubits are about 107 c and 173 c according to the golden sequence 3 x 3 = 9, 4 x 4 = 16, 5 x 5 = 25, 41, 66, 107, 173, 280 ... while the numbers of the oblique measurements are obtained from the golden sequence 12, 20, 32, 52, 84, 136, 220, 356 ... The volume of the hemisphere is 3/5 of the volume of the pyramid according to the magic formula rendered above.
If the circle discovered by John Taylor was Re emerging from the Primary Hill, then our hemisphere was heaven enclosed in the same hill.
An alter ego of Hathor was the sky goddess Nut bending over the earth - her husband Geb - while standing on the eastern horizon and resting with her hands on the western horizon. The mother goddess of heaven bore the sunchild. Her symbol in the frame of the pyramid may have been the western-eastern hemicircle of the golden hemisphere, as shown in figure 7, while her womb, wherein the sunchild is raised, may have been symbolized by the apex of the hemicircle. - If there is a hidden chamber in the Great Pyramid at Giza it might well lie on top of the imaginary hemisphere, 173 cubits or 90.6 m above the base.
We find several forms which may be associated with mythical elements or even deities:
pyramid - Primary Hill
square of the base - earth - Geb
eastern-western hemicircle - heaven - Nut, Mother Goddess
of Heaven
apex of the hemicircle - zenith - her womb
hemisphere - sky - Hathor
Taylor circle - sun - Re emerging from the Primary Hill
Goyon Pyramid - Primordial One
Taylor and Golden Pyramid - polarity, emerging from the
Primordial One, creating all the many forms and things
The pyramid may symbolize the origin of our present world and thus look back in time. It may also be a promise of another world to come when this one has passed away and thus look forward in time:
Primary Hill - promise of a new world to come
Geb - promise of a new earth
Nut - promise of a new heaven
Sunchild - promise of a new sun
Hathor - promise of a new sky
Re and Hathor, emerging from the Primary Hill - initiating
a new world, founding another golden age
as man and wife - ensuring the continuation of life
Re, Hathor, Nut, Geb and the Sunchild were related in a most complex way: Re was sometimes called the husband of Hathor and sometimes her father, whereas the oldest legends suggest that he was her son. Hathor and her alter ego Nut may thus have been the Mother Goddess of earlier times. Nut and Geb had five children, among them the sunchild Horus the Elder. As the sun, Re and Horus were the same god. Another child of Nut and Geb was Osiris. This god was seen and worshipped in the large and beautiful constellation of Orion. Several passages of the Pyramid Texts and the Book of the Dead confirm that Re, Horus and Osiris were the same god again. Re and Osiris were united as Re-Osiris who was depicted as a ram carrying the solar disk on his horns. This god (Re-Osiris) was also the Pharaoh being reborn as Re in the morning and Osiris in the evening.
The pyramid did not only look backwards and forwards in time.
It also had a function in the present: as the tomb of the Pharaoh
and the place where he was reborn as a god.
While his body lay in the King's Chamber his soul may have
lived in the hypothetical Sun Chamber.
The pyramid was his House of Eternity and was even considered
to be the body of the deified king.
When he was to leave his pyramid as Re he may have done so
by means of the Taylor transformation shown in figure 5 above,
and when he was to leave his House of Eternity as Osiris his
soul was guided by the southern pit of the King's Chamber.
According to Robert Bauval this pit points to the then
culmination of Al Nitak in Orion, while the pyramid itself
is an earthly representation of the very same star when seen
in context with some further pyramids arranged in the pattern
of Orion:
pyramids of Awyat-el Aryan - Betelgeuse
Khufu pyramid - Al Nitak (left belt-star)
Khafre pyramid - Al Nilam (middle belt star)
Menkaure pyramid - Al Mintaka (right belt-star)
Djedefre pyramid in Abu Roash - Rigel
What was the Great Pyramid?
The tomb and memorial of a king?
A sign of his power and evidence of his megalomania?
Or was the building of such a monument a way to unite Egypt
by means of a great task involving more or less the whole people
as explained by Kurt Mendelssohn?
Or was it a religious work? An icon of creation? A promise
of a new world to come when this one has passed away? and
a pledge for a new life for both the king and his people?
(for what is a king without his people?)
Did it belong to the sun? Or was it related to the stars?
to Al Nitak and Alpha Draconis, Sirius and Beta Ursae Minoris
which are according to Robert Bauval sigthed by the pits of
the King's Chamber and the so-called Queen's Chamber?
Did the pyramids listed above represent Orion, also as stated
by Bauval? Did the many graves, mastabas and pyramids on the
western bank of the river Nile symbolize stars and constellations
bordering on the Milky Way? heming the heavenly Nile? where
the souls of the deceased were believed to find a new life and
home?
Does the Great Pyramid possibly stand on the site of a
predynastic sanctuary? On a low hill once also used for
astronomical purposes? Does the meaning of the pyramid go back
to an earlier religion? Might the Primeval Goddess have survived
in Nut and her daughters Isis and Nephtys?
Or is the pyramid a document of a scientific achievement?
possibly based on even earlier knowledge?
And, more generally, was it a testimony to the skills and
abilites of a people at the close of the Stone Age?
It might well have been all of these.
Preview
In chapter 23, line 14, of the Book of the Dead translated by Erik Hornung King Wenefer/Osiris utters the enigmatic words:
"Ich bin der grosse weibliche Orion"
"I am the great female Orion"
Was Orion once a woman? the Mother Goddess of earlier times?
Orion her body? Gemini and Taurus her raisen arms? Sirius her
gourd filling the Nile with her life-spending water? This and
many further topics will be discussed in the following chapter.
Bibliography
DAVID EUGENE SMITH, History of Mathematics, Dover Publications
New York 1923/51/58
GEORGES GOYON, Die Cheops-Pyramide, Geheimnis und Geschichte,
Bergisch Gladbach 1974
MENDELSSOHN KURT, Das Raetsel der Pyramiden, Bergisch Gladbach
1974
JEAN-PHILIPPE LAUER, Das Geheimnis der Pyramiden, Baukunst
und Technik, Muenchen Berlin 1980
LUCIE LAMY, egyptian mysteries, New light on ancient knowledge,
Thames and Hudson 1981/89
KARLHEINZ SCHUESSLER, Die aegyptischen Pyramiden, Erforschung,
Baugeschichte und Bedeutung, DuMont Buchverlag Koeln 1983/89
ERIK HORNUNG, Tal der Koenige, Artemis Zuerich 1985
RAINER STADELMANN, Die aegyptischen Pyramiden, Vom Ziegelbau
zum Weltwunder, Verlag Philipp von Zabern Mainz am Rhein 1985
WOLF MEYER-CHRISTIAN, Der 'Pythagoras' in Aegypten am Beginn
des Alten Reiches, Mitteilungen des Deutschen Archaeologischen
Institutes, Abteilung Kairo, Band 43, 1987
ERIK HORNUNG, Geist der Pharaonenzeit, Artemis Zuerich Stuttgart
1989
ERIK HORNUNG, Das Totenbuch der Aegypter, Artemis Zuerich
Stuttgart 1990
RAINER STADELMANN, Die grossen Pyramiden von Giza, Adeva Wien
1990
RICHARD H. WILKINSON, Symbol & Magic in Egyptian Art, Thames
and Hudson 1994
ROBERT BAUVAL & ADRIAN GILBERT, Das Geheimnis des Orion, List
Verlag Muenchen Leipzig 1994
W.S. ANGLIN, J. LAMBEK, The Heritage of Thales, Readings in
Mathematics, Springer 1995
PETER JANOSI, Die Pyramidenanlagen der Koeniginnen, Verlag der
Oesterreichischen Akademie der Wissenschaften, Wien 1996
JEAN KERISEL, Genie et dÇmesure d'un Pharaon: KhÇops, Editions
Stock 1996
NANCY THOMAS, The American Discovery of Ancient Egypt, Museum
Associates, Los Angeles County Museum of Art 1996
Some of my writings, published in small editions:
Die Sonnenkammer, Zuerich 1992;
Wie der Baumeister des Cheops
den Kreis anging, Zuerich 1994;
Die Cheops-Pyramide als Ikone
der Schoepfung, Zuerich 1995;
Erbe der Steinzeit, Zuerich 1995
homepage